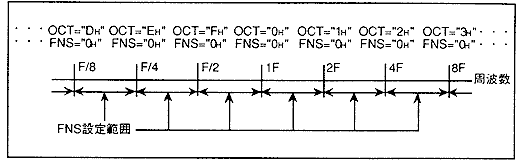
This register has a more detailed sound frequency setting function between the upper and lower octaves of "OCT". If both the "FNS" and "OCT" values are "0H", the pitch will match the sampling source. The relationship between the "FNS" and "OCT" values is shown in Figure 4.45. Figure 4.45 Relationship between OCT and FNS
The actual pitch (n) is calculated by the formula shown below.
The value obtained by this formula is expressed in cents. Here, I would like to explain about cents. One cent is 2 1/1200 = 1.000577789 times. Also, one octave is 1200 cents. At n cents, 2 for the original frequency It becomes double {= (1.000577789) n}. Therefore, Fn [Hz] can be calculated by the following formula to obtain the frequency of a sound n cents higher than the sound of the basic frequency Fo [Hz].
The actual frequency for the number of cents at this time is shown in Table 4.12.The "FNS" value at the time of P [Cent] can be calculated by the following formula.
From this formula, it is possible to output at any frequency by setting each parameter as shown in Table 4.13. Table 4.13 FNS.OCT parameter table| Note name | NOTE number | PITCH [Cent] | FNS [9: 0] [DEC] | FNS [9: 0] [HEX] | OCT [3: 0] [HEX] |
| B3 | 59 | 1100 | 909.1 | 38D | F |
| C4 | 60 | 0 | 0.0 | 0 | 0 |
| C4 # | 61 | 100 | 60.9 | 03D | 0 |
| D4 | 61 | 200 | 125.4 | 07D | 0 |
| D4 # | 63 | 300 | 193.7 | 0C2 | 0 |
| E4 | 64 | 400 | 266.2 | 10A | 0 |
| F4 | 65 | 500 | 342.9 | 157 | 0 |
| F4 # | 66 | 600 | 424.2 | 1A8 | 0 |
| G4 | 67 | 700 | 510.3 | 1FE | 0 |
| G4 # | 68 | 800 | 601.5 | 25A | 0 |
| A4 | 69 | 900 | 698.2 | 2BA | 0 |
| A4 # | 70 | 1000 | 800.6 | 321 | 0 |
| B4 | 71 | 1100 | 909.1 | 38D | 0 |
| C5 | 72 | 0 | 0.0 | 0 | 1 |
