Demo program A

Bounding Cube

Here, in order to summarize the flow up to now, I will introduce a slightly complicated program that displays polygons using the functions that have appeared so far.

So far, I have explained the following.

Drawing: Definition of polygons (Chapter 2)
Light source: Setting of light source and change of polygon surface by light source (Chapter 3)
Coordinate system: Coordinate system in Sega Saturn (Chapter 4)
Modeling transformations: object rotation, movement, scaling, etc. (Chapter 4)
Drawing area: Window and clipping (Chapter 4)

These are relatively common ideas in 3D graphics, regardless of hardware (although the functions used are different, of course).
Please read the following chapters after understanding these.
From the next chapter onward, we will mainly explain the ideas and special functions unique to Sega Saturn.

The demo program "demo_A" uses the SGL library functions that appeared from drawing to coordinate conversion in combination.
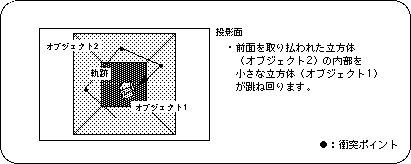
In the demo, a small cube polygon bounces around in a room represented by a cube polygon with all faces facing inward (not drawn when viewed from the outside).
Collision detection between a room and a small cube is processed by a simple conditional branch (XYZ coordinate value).

Figure A-1 Operation image of demo A

List A-1 demo_A: Demo Program A

/ * ------------------------------------------------ ---------------------- * /
/ * Cube Action * /
/ * ------------------------------------------------ ---------------------- * /
#include "sgl.h"

#define REFLECT_EXTENT to FIXED (85.0)
#define XSPD toFIXED (1.5)
#define YSPD to FIXED (2.0)
#define ZSPD to FIXED (3.0)

extern PDATA PD_PLANE1, PD_PLANE2;

void ss_main (void)
{
	static ANGLE ang1 [XYZ], ang2 [XYZ];
	static FIXED pos1 [XYZ], pos2 [XYZ], delta [XYZ], light [XYZ];

	slInitSystem (TV_320x224, NULL, 1);
	slPrint ("demo A", slLocate (9,2));

	ang1 [X] = ang1 [Y] = ang1 [Z] = DEGtoANG (0.0);
	ang2 [X] = ang2 [Y] = ang2 [Z] = DEGtoANG (0.0);
	pos1 [X] = pos2 [X] = toFIXED (0.0);
	pos1 [Y] = pos2 [Y] = toFIXED (0.0);
	pos1 [Z] = pos2 [Z] = toFIXED (100.0);
	delta [X] = XSPD, delta [Y] = YSPD, delta [Z] = ZSPD;
	light [X] = slSin (DEGtoANG (30.0));
	light [Y] = slCos (DEGtoANG (30.0));
	light [Z] = slSin (DEGtoANG (-30.0));

	while (-1) {
		slLight (light);
		slPushMatrix ();
		{
			slTranslate (pos1 [X], pos1 [Y], pos1 [Z] + toFIXED (270.0));

			pos1 [X] + = delta [X];
			pos1 [Y] + = delta [Y];
			pos1 [Z] + = delta [Z];

			if (pos1 [X]> REFLECT_EXTENT) {
				delta [X] = -XSPD, pos1 [X]-= XSPD;
			} else if (pos1 [X] <-REFLECT_EXTENT) {
				delta [X] = XSPD, pos1 [X] + = XSPD;
			}
			if (pos1 [Y]> REFLECT_EXTENT) {
				delta [Y] = -YSPD, pos1 [Y]-= YSPD;
			} else if (pos1 [Y] <-REFLECT_EXTENT) {
				delta [Y] = YSPD, pos1 [Y] + = YSPD;
			}
			if (pos1 [Z]> REFLECT_EXTENT) {
				delta [Z] = -ZSPD, pos1 [Z]-= ZSPD;
			} else if (pos1 [Z] <-REFLECT_EXTENT) {
				delta [Z] = ZSPD, pos1 [Z] + = ZSPD;
			}

			slRotX (ang1 [X]);
			slRotY (ang1 [Y]);
			slRotZ (ang1 [Z]);
			ang1 [X] + = DEGtoANG (3.0);
			ang1 [Y] + = DEGtoANG (5.0);
			ang1 [Z] + = DEGtoANG (3.0);
			slPutPolygon (& PD_PLANE1);
		}
		slPopMatrix ();
		
		slPushMatrix ();
		{
			slTranslate (pos2 [X], pos2 [Y], pos2 [Z] + toFIXED (170.0));
			slRotY (ang2 [Y]);
			slRotX (ang2 [X]);
			slRotZ (ang2 [Z]);
			slPutPolygon (& PD_PLANE2);
		}
		slPopMatrix ();

		slSynch ();
	}
}

Flow A-1 sample_1_6: Flowchart of demo program A

From the next chapter, we will explain the contents in more detail, including the hierarchical matrix.
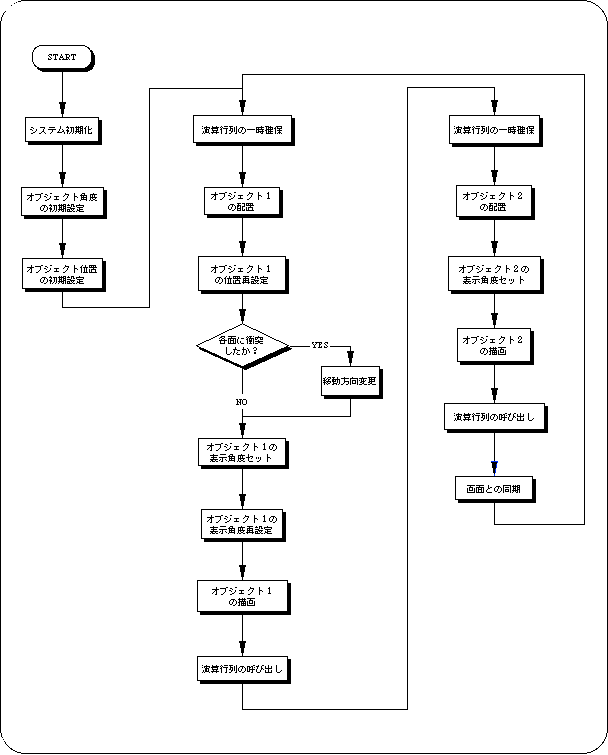
In particular, the idea of hierarchical structure using stacks is an important factor in 3D graphics, so please read it carefully or refer to specialized books to understand it.