<5/30> SGL Programmer's Tutorial / 4. Coordinate transformation

★ SGL User's Manual ★ PROGRAMMER'S STRUCT

▲ Back ｜ Forward ▼

PROGRAMMER'S STRUCT

4. Coordinate transformation

This chapter describes the basic idea of 3D graphics and the subroutines that realize it. In this chapter, we will mainly use a mathematical method called coordinate transformation. It may be difficult to read because it uses a lot of unusual methods such as determinant calculation, but it is the basis of 3D graphics, so please read and understand it many times.
The objects projected by 3D graphics are roughly defined by the following four.

Coordinate system → Determines the position and orientation of objects and viewpoints.
Projection transformation → Defines how the image is projected on the projection surface.
Modeling transformation → Defines movement, rotation, and scaling within the coordinate system.
Viewing transformation → Define the viewpoint and its movement (see “ Chapter 6 Camera ” for details).

By combining these four, 3D graphics can display images on a monitor. Therefore, in this chapter, we will explain the three in order, excluding the viewing transformation, and then add more detailed explanations.

4-1. Coordinate system

Sega Saturn uses a 3D coordinate system, which is generally called the right-handed coordinate system. This refers to a coordinate system in which the positive direction of the Y axis is at the bottom of the screen and the positive direction of the X axis is at the right of the screen when the positive direction of the Z axis is set at the back of the screen. In addition, the direction of rotation is positive (clockwise) with respect to the axis.

<Fig. 4-1 Coordinate system used by Sega Saturn>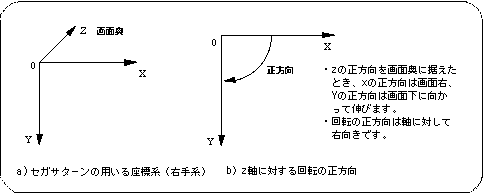

Apart from this, SGL has a 2D coordinate system called screen coordinates that corresponds to the TV monitor and screen mode (resolution). It is mainly used for dealing with 2D graphics such as scrolls and sprites, but it is also used when setting windows in the “4-5 window”.

<Fig. 4-2 Screen coordinate system>

4-2. Projection transformation

We will explain how the coordinates appear on the screen and explain how to set the projection.

Perspective projection

This section describes the perspective projection that is the basis of the transformation. First, set the viewpoint, and the projection result when there is a cube placed perpendicular to the line of sight on the extension of that viewpoint is shown in the figure below.

<Fig. 4-3 Concept of projection>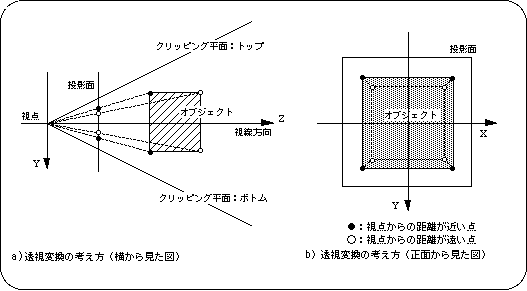

In perspective projection, an image is defined as a mapping to a plane called the projection plane. Think of a projection plane as a screen that projects a shadow puppet.
The point of the object is drawn at the intersection of the line segment connecting the viewpoint and the point of the object and the projection plane. By performing this operation on all the points of the object in the space, the space is drawn on the projection plane for the first time.

Figure 4-4 Projection plane in SGL

The projection plane in SGL means the TV monitor. After the objects placed in the virtual 3D space are perspectively projected, they are mapped to the screen coordinate system and drawn on the TV monitor.

Viewing volume

The range projected on the projection surface is called the viewing volume.
In the case of SGL, there are angles of view and display level as parameters that control this viewing volume.
Here, I will introduce these two.

1) Angle of view

Perspective is a parameter that determines how wide an image is projected on the projection surface in the left-right direction with the viewpoint as the origin.
Increasing this value will increase the density of the objects projected onto the projection plane, giving the image just as if you were looking through a fisheye lens.
The vertical spread is determined by the angle of view value and the resolution according to the screen mode.

<Fig. 4-5 Angle of view image model>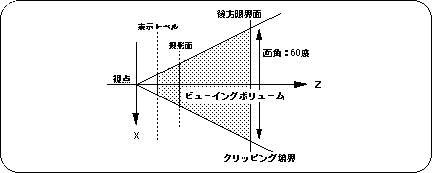

To change the perspective projection settings on SGL, use the function “slPerspective”.

[Void slPerspective (ANGLE perspective_angle);]

By changing the parameters of this function, you can control the spatial area projected on the projection plane.
Substitute the angle value (10 <angle <160) that determines the spatial area to be projected into the parameter. If it deviates from this value range, it will overflow.

<Fig. 4-6 Difference in image due to angle of view>

2) Display level

The display level is a parameter for determining the level behind the projection plane and the level to be projected on the projection plane.
Objects behind the projection plane are also projected onto the projection plane in the same way as the images behind the projection plane.

The display level is set by the function “slZdspLevel”.
The display level is determined by the position of the division point between the viewpoint and the projection plane.

[Void slZdspLevel (Uint16 level);]

Determines the display level of the viewing volume.
Substitute the values in the table below for the parameters according to the display level.

Table 4-1 Display level substitution value (level)
Display level
1/2 1/4 1/8
Substituted value 1 2 3

**Table 4-1 Display level substitution value (level)**
	Display level
1/2	1/4	1/8
Substituted value	1	2	3

The figure below is a display level image model.

Figure 4-7 Display level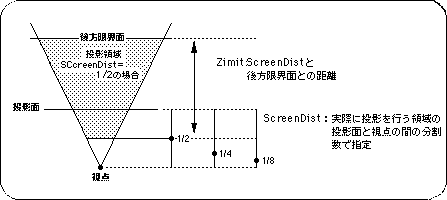

Listing 4-1 below shows what the cube looks like by placing the cube in the center of the screen and changing the angle of view value, which is a perspective parameter, between 20 and 160 degrees.

Listing 4-1 sample_4_2: Changes in video due to perspective

/ * ------------------------------------------------ ---------------------- * /
/ * Perspective Control * /
/ * ------------------------------------------------ ---------------------- * /
#include "sgl.h"

extern PDATA PD_CUBE;

void ss_main (void) {
	static ANGLE ang [XYZ];
	static ANGLE angper [XYZ];
	static FIXED pos [XYZ];
	static ANGLE tmp = DEGtoANG (90.0);
	static ANGLE adang = DEGtoANG (0.5);

	slInitSystem (TV_320x224, NULL, 1);
	slPrint ("Sample program 4.2", slLocate (6,2));

	ang [X] = DEGtoANG (30.0);
	ang [Y] = DEGtoANG (45.0);
	ang [Z] = DEGtoANG (0.0);
	pos [X] = toFIXED (50.0);
	pos [Y] = toFIXED (40.0);
	pos [Z] = toFIXED (20.0);

	slPrint ("Perspective:", slLocate (4,5));
	while (-1) {
		slPerspective (tmp);
		slPrintHex (slAng2Dec (tmp), slLocate (18,5));

		tmp + = adang;
		if (tmp> DEGtoANG (160.0)) 
			adang = DEGtoANG (-0.5);
		if (tmp <DEGtoANG (20.0))
			adang = DEGtoANG (0.5);

		slPushMatrix ();
		{
			FIXED dz;

			dz = slDivFX (slTan (tmp >> 1), toFIXED (170.0));
			slTranslate (pos [X], pos [Y], pos [Z] + dz);
			slRotX (ang [X]);
			slRotY (ang [Y]);
			slRotZ (ang [Z]);
			slPutPolygon (& PD_CUBE);
		}
		slPopMatrix ();

		slSynch ();
	}
}

Flow 4-1 sample_4_2: Flowchart of image change due to perspective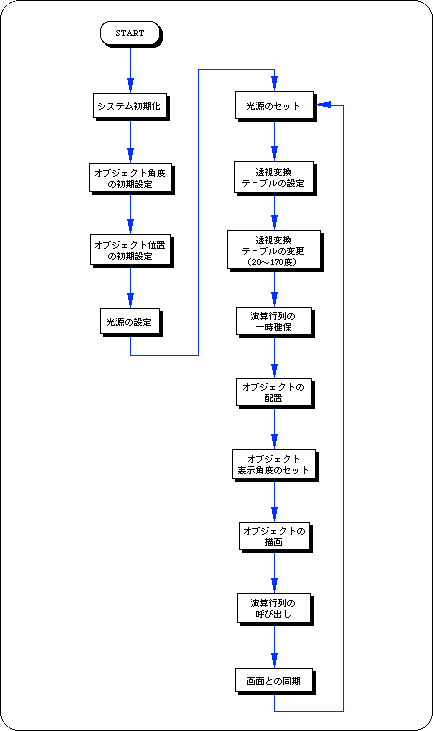

4-3. Modeling transformation

This section describes the placement and transformation of objects in space. There are three types of conversions for objects: move, rotate, and scale.
By using this, you can arrange objects freely.
Next, I will explain each conversion operation in order with a sample program.

<Fig. 4-8 Various conversion operations for objects>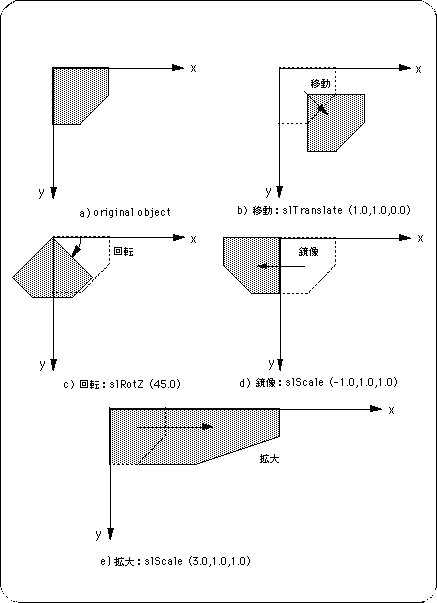

Note) Angles and variables are shown in degrees and floating for convenience.

Object rotation

To rotate an object in space, use the library functions “slRotX, slRotY, slRotZ”. Controls the rotation corresponding to the coordinate axes at the end of each function name.
Object rotation is achieved by multiplying the coordinates of each vertex of the object by a transformation matrix called the rotation matrix.

[Void slRotX (ANGLE angx);]

Adds rotation around the X axis to the object. Substitute the rotation angle value for the parameter.

[Void slRotY (ANGLE angy);]

Adds rotation around the Y axis to the object. Substitute the rotation angle value for the parameter.

[Void slRotZ (ANGLE angz);]

Adds rotation around the Z axis to the object. Substitute the rotation angle value for the parameter.

List 4-2 below is a program that rotates the square polygon drawn in Listing 2-1 in Chapter 2 on the Y axis using the library function “slRotY” (single axis rotation). The rotation matrix is expressed by the following equation.

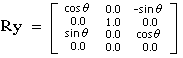
<List 4-2 sample_4_3_1: Square polygon single axis rotation routine>

/ * ------------------------------------------------ ---------------------- * /
/ * Rotation of 1 Polygon [Y axis] * /
/ * ------------------------------------------------ ---------------------- * /
#include "sgl.h"

extern PDATA PD_PLANE1;

void ss_main (void)
{
	static ANGLE ang [XYZ];
	static FIXED pos [XYZ];

	slInitSystem (TV_320x224, NULL, 1);
	slPrint ("Sample program 4.3.1", slLocate (9,2));

	ang [X] = ang [Y] = ang [Z] = DEGtoANG (0.0);
	pos [X] = toFIXED (0.0);
	pos [Y] = toFIXED (0.0);
	pos [Z] = toFIXED (220.0);

	while (-1) {
		slPushMatrix ();
		{
			slTranslate (pos [X], pos [Y], pos [Z]);
			slRotX (ang [X]);
			slRotY (ang [Y]);
			slRotZ (ang [Z]);
			ang [Y] + = DEGtoANG (5.0);
			slPutPolygon (& PD_PLANE1);
		}
		slPopMatrix ();

		slSynch ();
	}
}

Flow 4-2 sample_4_3_1: Square polygon single axis rotation routine flowchart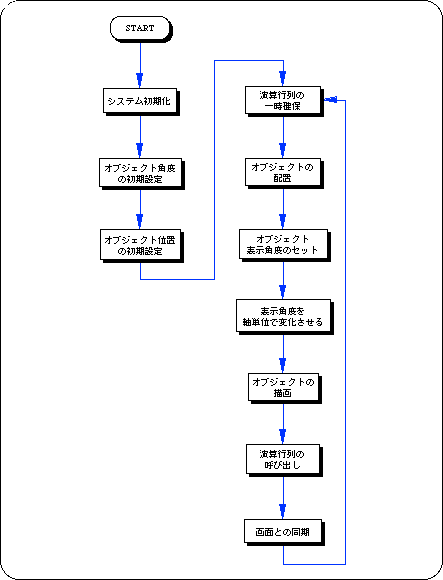

List 4-3 below is a program to realize biaxial rotation. Rotate the square polygon on two axes, the X axis and the Y axis.
The actual operation is the same for single-axis rotation, 2-axis rotation, or 3-axis rotation. By manipulating the angle value of the rotation operation function corresponding to each axis, the object is drawn with rotation applied.

Listing 4-3 sample_4_3_2: Square polygon 2-axis rotation routine

/ * ------------------------------------------------ ---------------------- * /
/ * Rotation of 1 Polygon [X & Y axis] * /
/ * ------------------------------------------------ ---------------------- * /
#include "sgl.h"

extern PDATA PD_PLANE1;

void ss_main (void)
{
	static ANGLE ang [XYZ];
	static FIXED pos [XYZ];

	slInitSystem (TV_320x224, NULL, 1);
	slPrint ("Sample program 4.3.2", slLocate (9,2));

	ang [X] = ang [Y] = ang [Z] = DEGtoANG (0.0);
	pos [X] = toFIXED (0.0);
	pos [Y] = toFIXED (0.0);
	pos [Z] = toFIXED (220.0);

	while (-1) {
		slPushMatrix ();
		{
			slTranslate (pos [X], pos [Y], pos [Z]);
			slRotX (ang [X]);
			slRotY (ang [Y]);
			slRotZ (ang [Z]);
			ang [X] + = DEGtoANG (4.0);
			ang [Y] + = DEGtoANG (2.0);
			slPutPolygon (& PD_PLANE1);
		}
		slPopMatrix ();

		slSynch ();
	}
}

Move objects

To move an object in space with SGL, use the library function "slTranslate".
By substituting the amount of movement for each XYZ axis from the local point as a parameter, the object can be displayed at any coordinate in 3D space.

[Void slTranslate (FIXED tx, ty, tz);]

Moves the object to the specified coordinates and displays it.
Substitute the defined coordinates or the amount of movement for each XYZ axis from the local point into the parameter.

Listing 4-4 below uses the library function “slTranslate” to achieve movement parallel to the X-axis. The Sin value is used to control the movement parameters. The change in the angle value tmp controls the change in the X coordinate value.
The translation by “slTranslate” is expressed by the following equation.

Listing 4-4 sample_4_3_3: Square polygon translation routine

/ * ------------------------------------------------ ---------------------- * /
/ * Parallel Translation of 1 Polygon [X axis] * /
/ * ------------------------------------------------ ---------------------- * /
#include "sgl.h"

#define POS_Z 50.0

extern PDATA PD_PLANE1;

void ss_main (void)
{
	static ANGLE ang [XYZ];
	static FIXED pos [XYZ];
	static ANGLE tmp = DEGtoANG (0.0);

	slInitSystem (TV_320x224, NULL, 1);
	slPrint ("Sample program 4.3.3", slLocate (9,2));

	ang [X] = ang [Y] = ang [Z] = DEGtoANG (0.0);
	pos [X] = toFIXED (0.0);
	pos [Y] = toFIXED (0.0);
	pos [Z] = toFIXED (220.0);

	while (-1) {
		slPushMatrix ();
		{
			slTranslate (pos [X], pos [Y], pos [Z]);
			slRotX (ang [X]);
			slRotY (ang [Y]);
			slRotZ (ang [Z]);
			tmp + = DEGtoANG (5.0);
			pos [X] = slMulFX (toFIXED (POS_Z), slSin (tmp));
			slPutPolygon (& PD_PLANE1);
		}
		slPopMatrix ();

		slSynch ();
	}
}

<Flow 4-3 sample_4_3_3: Square polygon translation flowchart>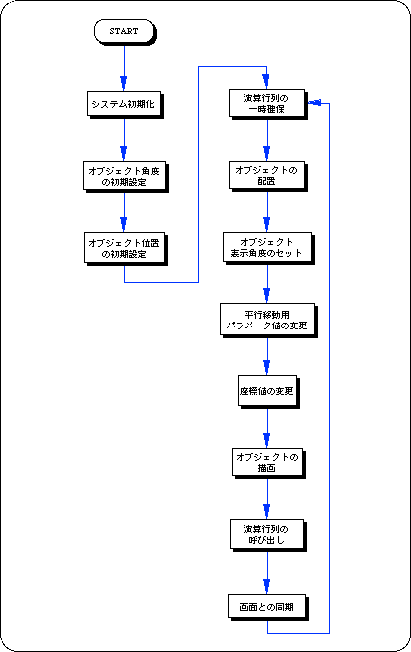

Enlargement / reduction of objects

To scale an object in space with SGL, use the library function "slScale". The parameters are passed as a scale ratio for each axis.

[Void slScale (FIXED sx, sy, sz);]

Scales and displays the object by each axis.
Substitute the scale value (arbitrary magnification) for each axis direction of the XYZ axes for the parameter.
The object changes depending on the scale value as shown in the table below.

Table 4-2 Changes in objects due to scale values
Parameter range
scale <0.0 scale = 0.0 0.0 <scale <1.0 scale = 1.0 1.0 <scale
Conversion result Mirror image Disappearance Shrink 1x expansion
Note) "scale" refers to the scale parameter.

Changes in objects due to scale values

**Table 4-2 Changes in objects due to scale values**
	Parameter range
scale <0.0	scale = 0.0	0.0 <scale <1.0	scale = 1.0	1.0 <scale
Conversion result	Mirror image	Disappearance	Shrink	1x	expansion

If the scale value is 0.0, the object will be drawn as having no thickness in the scaled axial direction.
Also, for negative values less than 0.0, the object is drawn as a mirror image with respect to the scaled axial direction.

Listing 4-5 below shows the scaling programs. The scale ratio of the square polygon in the X-axis direction and the Y-axis direction is changed.

Listing 4-5 sample_4_3_4: Square polygon scaling routine

/ * ------------------------------------------------ ---------------------- * /
/ * Expansion & Reduction of 1 Polygon [X & Y axis] * /
/ * ------------------------------------------------ ---------------------- * /
#include "sgl.h"

extern PDATA PD_PLANE1;

void ss_main (void)
{
	static ANGLE ang [XYZ];
	static FIXED pos [XYZ];
	static FIXED sclx, scly, sclz, tmp = toFIXED (0.0);
	static Sint16 flag = 1;

	slInitSystem (TV_320x224, NULL, 1);
	slPrint ("Sample program 4.3.4", slLocate (9,2));

	ang [X] = ang [Y] = ang [Z] = DEGtoANG (0.0);
	pos [X] = toFIXED (0.0);
	pos [Y] = toFIXED (0.0);
	pos [Z] = toFIXED (220.0);
	sclx = scly = sclz = toFIXED (1.0);

	while (-1) {
		slPushMatrix ();
		{
			slTranslate (pos [X], pos [Y], pos [Z]);
			slRotX (ang [X]);
			slRotY (ang [Y]);
			slRotZ (ang [Z]);
			if (flag == 1) tmp + = toFIXED (0.1);
			else tmp-= toFIXED (0.1);
			if (tmp> toFIXED (1.0)) flag = 0;
			if (tmp <toFIXED (-1.0)) flag = 1;
			slScale (sclx + tmp, scly --tmp, sclz);
			slPutPolygon (& PD_PLANE1);
		}
		slPopMatrix ();

		slSynch ();
	}
}

<Flow 4-4 sample_4_3_4: Square polygon enlargement / reduction flowchart>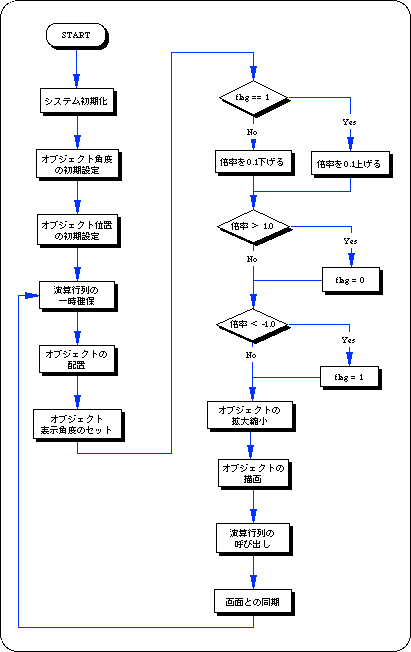

Special modeling transformation

Here, I will introduce a library function that performs a slightly special modeling conversion operation. All of the items introduced here add a rotation operation to the object data, but the parameter settings are different from the above-mentioned library function for rotation operation.

[Void slRotXSC (FIXED sin, FIXED cos);]

Substitute the sine value and cosine value to add rotation around the X axis.
Substitute the Sin value and Cos value as FIXED type values for the parameters, respectively.

[Void slRotYSC (FIXED sin, FIXED cos);]

Substitute the sine value and cosine value to add rotation around the Y axis. Substitute the Sin value and Cos value as FIXED type values for the parameters, respectively.

[Void slRotZSC (FIXED sin, FIXED cos);]

Substitute the sine value and cosine value to add rotation around the Z axis.
Substitute the Sin value and Cos value as FIXED type values for the parameters, respectively.

[Void slRotAX (VECTOR vx, vy, vz, ANGLE anga);]

Add rotation around an arbitrary axis through the origin (axis units are specified as vector values).
Substitute the unit vector value (XYZ) representing the rotation axis and the rotation angle value for the parameters.
Substitute a vector value that represents the axis of rotation so that it is always a unit vector.
A unit vector is a vector whose magnitude is always 1.

Difference in results due to conversion order

In the case of 3D graphics, various transformations represented by modeling transformations are performed using a transformation matrix called a matrix. Therefore, if you do not perform the conversion operation after understanding the conversion order, the object may be drawn with a different result than intended. The following figures are both rotation and movement conversion operations, but the final drawing results are significantly different because the conversion order is different.

<Fig. 4-9 Difference in results due to conversion order>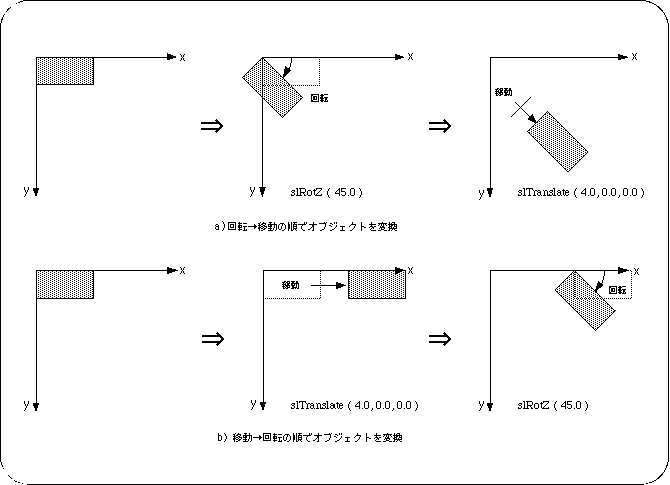

Note) Angles and variables are shown in degrees and floating for convenience.

4-4. Clipping

Clipping is the process of removing the part that extends beyond the display area (the area that is actually projected onto the projection surface) and making it invisible. SGL can use this idea to set a window for the projection plane. Therefore, I will explain the concept of clipping first, and then explain the actual window setting on SGL.

2D clipping

First, I will explain the concept of clipping with an example of 2D graphics. In the case of 2D graphics, you can switch between showing and hiding inside and outside the separated rectangular area.
The example below shows a display example when objects to be displayed are placed inside and outside the display area given as a rectangular area.

<Fig. 4-10 2D clipping example>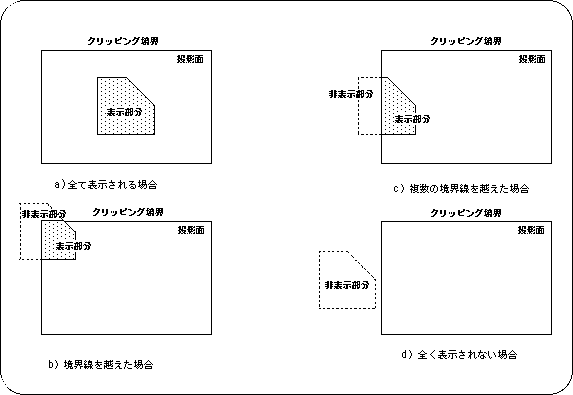

Note) When the projection plane closed by the clipping boundary is used as the display area

As shown in the figure above, the object to be clipped can be displayed / hidden inside or outside the clipping area. In the case of this example, if one object covers both clipping areas, part of the object (inside the area) will be displayed and part (outside the area) will not be displayed.

Note <BR> In some cases, due to problems with calculation speed and drawing speed, display / non-display may be switched depending on the ratio of one object included in the clipping area.

3D clipping

In 3D graphics, the perspective transformation matrix usually determines the visual field pyramid, and the inside of this pyramid is defined as the display area and the outside of the pyramid is defined as the non-display area. Objects in the display area are projected onto the projection plane and projected onto the monitor.
This field of view pyramid is clipped by a closed space (viewing volume) surrounded by the following six planes.

Left side of field of view	: Clipping plane (determined by angle of view)
Right side of field of view	: Clipping plane (determined by angle of view)
Top of field of view	: Clipping plane (determined by angle of view and screen mode)
Underside of the field of view	: Clipping plane (determined by angle of view and screen mode)
Front of field of view	: Forward limit plane (determined by the function “slZdspLevel”)
The back of the field of view	: Rear limit plane (determined by the parameter "Zlimit" in the function "slWindow")

In the case of SGL In addition to this, it is possible to add additional clip planes (see " Section 4.5: Window " for details).

Figure 4-11 Definition of display area by 3D clipping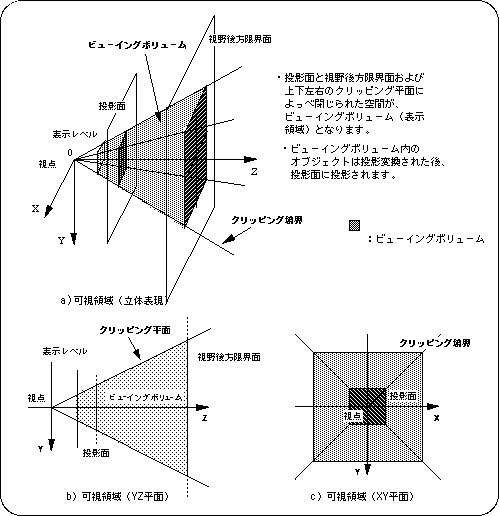

Figure 4-12 Example of 3D clipping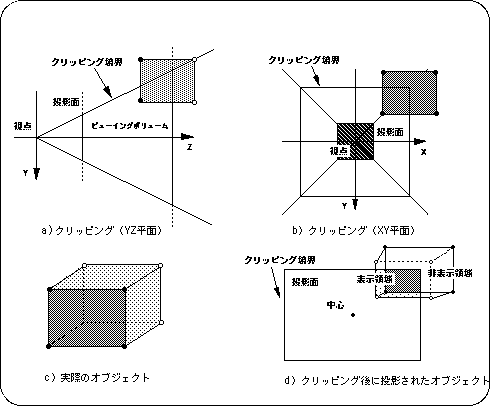

4-5. Window

In SGL, the concept of clipping can be used to set a rectangular area for display restrictions called a window with respect to the projection plane. Objects can be shown or hidden inside or outside this area.
Up to two windows can be held on one screen. One of these is set as the default window from the beginning. This window is the same size as the projection plane (TV monitor) and can be reset in the program.

Window concept

In SGL, windows are defined as shown below.

<Fig. 4-13 Window concept>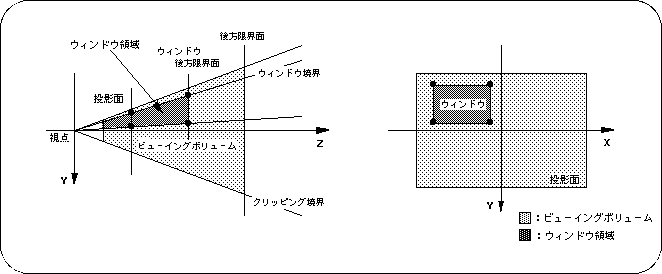

In SGL, a window is defined as a rectangular area in the projection plane. If this is interpreted three-dimensionally, it means the area that should be projected onto the rectangular area of the projection surface in the viewing volume (in the figure: dark shaded area). By specifying the window area, the display / non-display of the object is decided inside and outside this.
The window size can be set up to the same size as the projection plane.

Window settings in SGL

To actually set the window in SGL, use the library function "slWindow". In the initial state (without using slWindow), SGL has already set a resettable default window of the same size as the projection plane.

[Void slWindow (left, top, right, bottom, Zlimit, CENTER_X, CENTER_Y);]

The library function slWindow sets the window area on the projection plane. Each parameter sets the screen coordinates of the upper left and lower right of the window on the projection plane, the rear limit coordinates, and the screen coordinates that determine the line-of-sight direction. The figure below illustrates each parameter.

Figure 4-14 Meaning of parameters in “slWindow”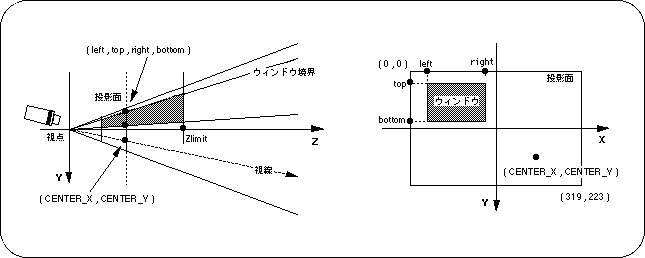

Note) left, top, right, bottom, CENTER_X, CENTER_Y indicate the XY coordinate values for the monitor.

The parameters of the library function “slWindow” are defined as follows.

[Sint 16 left, top, right, bottom]

The screen coordinate values of the upper left and lower right with respect to the projection plane (monitor) of the window are shown.
The range of values depends on the screen mode (maximum is the full size resolution by screen mode).
In the default window, the window size and monitor size are set to the same (maximum).

[Zlimit]

Specifies the projection limit of the window.
The projection limit value is a parameter for determining how much depth from the front limit plane specified by the function "slZdspLevel" is actually projected on the projection plane (designation of the rear limit plane). ..
If “Zlimit = -1” is assigned, the Zlimit value of the previously set window will be used.
If no window was previously set, the default window value (7FFF) will be used.

[CENTER_X, CENTER_Y]

It determines the line-of-sight direction and the parameters are expressed as screen coordinate values. By changing this value, it is possible to determine where on the screen the distant objects will converge.
This point is commonly referred to as the "vanishing point" in the world of 3D graphics.
In the default window, the "vanishing point" is set to the center of the screen.

About screen coordinates

Screen coordinates are a 2D coordinate system that corresponds to the TV monitor that is the projection plane.
The origin is on the upper left, the X-axis is on the right, and the Y-axis is on the bottom. The range of values varies depending on the screen mode, but it is usually expressed (horizontal: 320 x vertical: 224).

Figure 4-15 Differences in images due to CENTER_X and CENTER_Y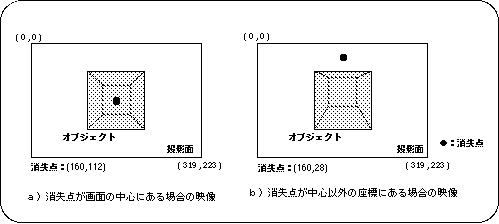

Note) Conditions such as objects and viewpoints are the same for both a) and b).

Reset the default window

If you want to set the default window again after rewriting the default window for some reason, enter the following value in the library function “slWindow”.
However, in the example below, it is assumed that the screen size is (width 320 x height 224).

Figure 4-16 Resetting the default window

● In screen mode (horizontal 320 x vertical 240)
slWindow (0,0,319,223,0x7FFF,160,112);
         | | |
         | | Vanishing point coordinate value: center of screen | Zlimit
         Window range indication coordinate value

The default window is a window that is the same size as your monitor.
The window size is the same size as the monitor (the value changes depending on the screen mode), the rear limit coordinate value is set to "0x7FFF", and the vanishing point is set in the center of the monitor.

Sample program

The figure below is an example of displaying an object by the sample program “sample_4_5” using a window. Object 1 is a rectangular plate polygon, and object 2 is a cube polygon, and they are arranged so that they intersect each other at a certain Z coordinate.
The display when a window is set using the library function "slWindow" is d) in the figure below. Object 1 is set to display outside the window area, and object 2 is set to display inside the window area (more on this setting later).

Figure 4-17 Example of object display using a window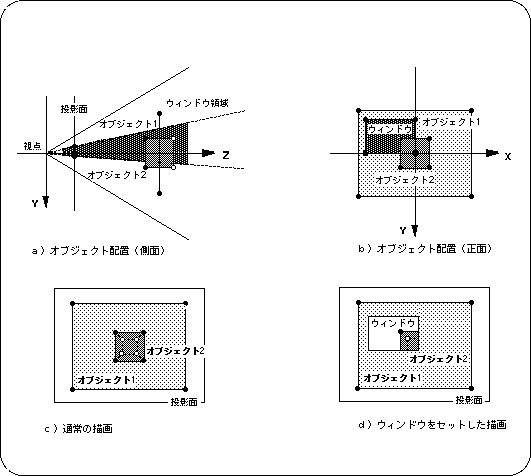

Note 1) Object 1 is displayed outside the window Note 2) Object 2 is displayed inside the window

In SGL, you can show / hide objects inside and outside the window. This switching can be set for each polygon plane as a polygon attribute.
Details will be given in "Chapter 7: Polygon Face Attributes", but here we will introduce the parts that correspond to polygon face attributes in the data file "polygon.c" used in the sample program.

Listing 4-7 polygon.c: Polygon attributes related to window display

/ * Omitted * /

ATTR attribute_PLANE [] = {
	ATTRIBUTE (Single_Plane, SORT_MIN, No_Texture, C_RGB (16,16,16), No_Gouraud, MESHoff | Window_Out, sprPolygon, No_Option),
	ATTRIBUTE (Single_Plane, SORT_MIN, No_Texture, C_RGB (00,31,31), No_Gouraud, MESHoff | Window_Out, sprPolygon, No_Option),
};

ATTR attribute_CUBE [] = {
	ATTRIBUTE (Single_Plane, SORT_MIN, No_Texture, C_RGB (31,31,31), No_Gouraud, MESHoff | Window_In, sprPolygon, No_Option),
	ATTRIBUTE (Single_Plane, SORT_MIN, No_Texture, C_RGB (31,00,00), No_Gouraud, MESHoff | Window_In, sprPolygon, No_Option),
	ATTRIBUTE (Single_Plane, SORT_MIN, No_Texture, C_RGB (00,31,00), No_Gouraud, MESHoff | Window_In, sprPolygon, No_Option),
	ATTRIBUTE (Single_Plane, SORT_MIN, No_Texture, C_RGB (00,00,31), No_Gouraud, MESHoff | Window_In, sprPolygon, No_Option),
	ATTRIBUTE (Single_Plane, SORT_MIN, No_Texture, C_RGB (31,31,00), No_Gouraud, MESHoff | Window_In, sprPolygon, No_Option),
	ATTRIBUTE (Single_Plane, SORT_MIN, No_Texture, C_RGB (00,31,31), No_Gouraud, MESHoff | Window_In, sprPolygon, No_Option),
};

/ * Omitted * /

Range of influence by windows

Only two functions "slWindow" can be used in one frame.
If you call the functions "slPutPolygon", "slPutSprite", etc., the first window will be used at that point, and you can only call "slWindow" once after that.
(Calling the above function changes the default window settings)

Only one window setting works at a time. Also, when the function "slWindow" is called, the priority is separated from the polygons (sprites) before it and those after that, and in this case, the later one is always given priority.

Listing 4-8 Window settings impact range

		: / * Wind 1 (default) * /
	slPutPolygon ( object1 );
		::
	slPutPolygon ( object2 );
		::
slWindow (.....); ←
		: / * Wind 2 * /
	slPutPolygon ( object3 );
		::
slWindow (.....); ← Error: / * Window 2 remains * /
	slPutPolygon ( object4 );
		::
	slPutPolygon ( object5 );
		::

In the case of the example, object1 and object2 are displayed first by the default window, and then window2 is set.
In response to this, the default window window 1 and the newly set window 2 appear on the projection plane.
Object3 drawn in this state will be affected by the new window.
Furthermore, when you run the slWindow, already two of the next error for that window is used, you will not be able to set a new one.
object4 and object5 are drawn on the projection plane under the influence of window 2.

Appendix SGL library functions that appeared in this chapter

In this chapter, the functions in the following table are explained.

Table 4-3 SGL library functions introduced in this chapter
Functional type
Function name
Parameters
function
void slPerspective ANGLE angp Settings of perspective conversion table
void slRotX ANGLE angx Rotation of polygon data around the X axis
void slRotY ANGLE angy Rotation of polygon data around the Y axis
void slRotZ ANGLE angz Rotation of polygon data around the Z axis
void slRotXSC FIXED sn, FIXED cs Rotation around the X axis by specifying Sin and Cos
void slRotYSC FIXED sn, FIXED cs Rotation around the Y axis by specifying Sin and Cos
void slRotZSC FIXED sn, FIXED cs Rotation around the Z axis by specifying Sin and Cos
void slRotAX FIXED vx, vy, cz, ANGLE a Rotation around an arbitrary axis passing through the origin (axis unit: vector)
void slScale FIXED sx, sy, sz Enlargement / reduction of polygon data
void slWindow lft, top, rgt, btm, Zlimit, CNTX, CNTY Wind setting
void slZdspLevel level Specifying the display level of the viewing volume

**Table 4-3 SGL library functions introduced in this chapter**
Functional type	Function name	Parameters	function
void	slPerspective	ANGLE angp	Settings of perspective conversion table
void	slRotX	ANGLE angx	Rotation of polygon data around the X axis
void	slRotY	ANGLE angy	Rotation of polygon data around the Y axis
void	slRotZ	ANGLE angz	Rotation of polygon data around the Z axis
void	slRotXSC	FIXED sn, FIXED cs	Rotation around the X axis by specifying Sin and Cos
void	slRotYSC	FIXED sn, FIXED cs	Rotation around the Y axis by specifying Sin and Cos
void	slRotZSC	FIXED sn, FIXED cs	Rotation around the Z axis by specifying Sin and Cos
void	slRotAX	FIXED vx, vy, cz, ANGLE a	Rotation around an arbitrary axis passing through the origin (axis unit: vector)
void	slScale	FIXED sx, sy, sz	Enlargement / reduction of polygon data
void	slWindow	lft, top, rgt, btm, Zlimit, CNTX, CNTY	Wind setting
void	slZdspLevel	level	Specifying the display level of the viewing volume

▲ Back ｜ Forward ▼

★ SGL User's Manual ★ PROGRAMMER'S STRUCT

4. Coordinate transformation

4-1. Coordinate system

4-2. Projection transformation

Viewing volume

4-3. Modeling transformation

Object rotation

Move objects

Enlargement / reduction of objects

Changes in objects due to scale values

Special modeling transformation

Difference in results due to conversion order

4-4. Clipping

2D clipping

3D clipping

4-5. Window

Window concept

Window settings in SGL

About screen coordinates

Reset the default window

slWindow (0,0,319,223,0x7FFF,160,112); | | | | | Vanishing point coordinate value: center of screen | Zlimit Window range indication coordinate value

Sample program

Range of influence by windows

Appendix SGL library functions that appeared in this chapter