5. Matrix

This chapter describes the matrix that is the basis for building 3D graphics.
In the first half, we will explain matrix operations and their concepts, and in the second half, we will explain the construction of objects using a hierarchical structure using a stack matrix.
In particular, the hierarchical structure of the matrix is an important element in 3D graphics representation by Sega Saturn, so please read and understand it carefully.

5-1. Matrix

A matrix is also called a matrix. This is a concept for treating a group of numbers as a group, unlike the operation of single numbers.

A matrix is a group of numbers in n rows and m columns, which is different from normal numerical operations, but it is also possible to perform four arithmetic operations between matrices (for details, refer to specialized books).
The figure below is an example of multiplication between 2-row x 2-column matrices.
In the case of SGL, a 4-row x 3-column matrix is used as the matrix variable to accurately represent the 3D space (to realize XYZ coordinate values and various conversion operations).

<Fig. 5-1 General concept of matrix and calculation example>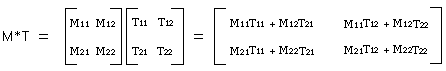

note)

M11 to M22 and T11 to T22 are ordinary variables

The modeling transformation explained in "Chapter 4 Coordinate Transformation " is also a new polygon vertex data string created by multiplying the polygon vertex data string represented as a matrix by various transformation matrices (rotation, movement, scale, etc.). is.

5-2. Object representation by hierarchical structure

This item explains the hierarchical structure representation of objects by a matrix using a stack. Simply put, this means having relationships between multiple objects. This relationship is commonly referred to as the parent-child structure .

stack

A stack is a structural model for efficiently handling a matrix. This is shown in Figure 5-2 , and the functions for doing this are “slPushMatrix” and “slPopMatrix”.
The matrix that exists at the lowest level in the stack is called the current matrix, and various matrix conversion operations are performed on the current matrix.

[Bool slPushMatrix (void);]

Copy the current current matrix to the lower stack and move the current matrix to the lower level at the same time. Used for temporary storage of the matrix.

[Bool slPopMatrix (void);]

Restores the temporarily saved upper matrix and moves the current matrix to the upper level.

The lower stack matrix is abandoned.

<Fig. 5-2 Stack image model>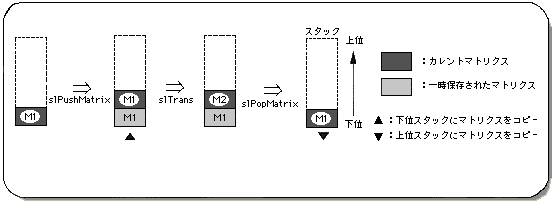

note)

The stack consists of 20 stacks, and the matrix is nested from the upper stack to the lower stack.

SGL holds a matrix called an environment matrix as a current matrix when the matrix environment is initialized.
This defines the basis of the 3D coordinate environment of SGL, and if it is rewritten, various conversion operations may not be performed correctly.
Therefore, SGL supports "slInitMatrix" as a library function that initializes the stack and various matrix variables.

[Void slInitMatrix (void)]

Initializes the stack and matrix variables. At this time, the environment matrix is secured on the stack as the current matrix.

Hierarchical concept

Figure 5-3 is an image model of a set of objects given a hierarchical structure. object1 is set to the shallowest level in the hierarchy, and object2 and object3 are defined at the following levels, respectively.

<Fig. 5-3 Image model of hierarchical structure>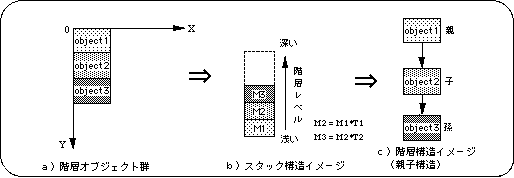

When using the hierarchical structure, the object behaves as shown in Figure 5-3. Figures 5-4 and 5-5 show the results of applying the same transformation to an object group that does not use a hierarchical structure and an object group that uses a hierarchical structure (parallel to each object in the X direction). Move).

<Fig. 5-4 Example of moving objects without using a hierarchical structure>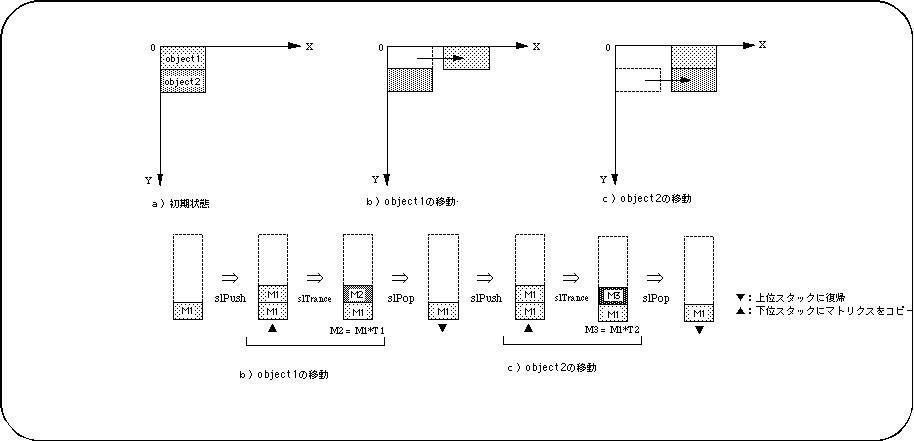

<Fig. 5-5 Example of object conversion using a hierarchical structure>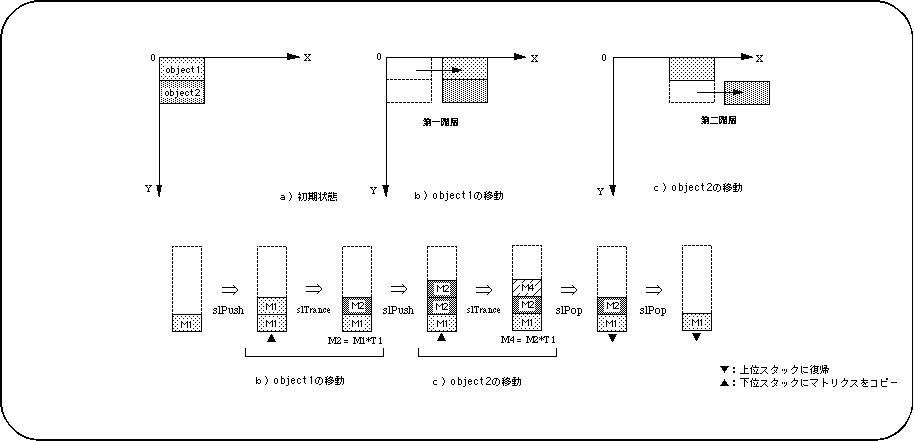

Definition of hierarchical structure by Sega Saturn

Next, referring to the sample program, we will explain how to realize a hierarchical structure in Sega Saturn.

Listing 5-1 sample_5_2: Hierarchical Matrix Definition

/ * ------------------------------------------------ ---------------------- * /
/ * Double Cube Circle Action * /
/ * ------------------------------------------------ ---------------------- * /
#include "sgl.h"

#define DISTANCE_R1 40
#define DISTANCE_R2 40

extern PDATA PD_CUBE;

static void set_star (ANGLE ang [XYZ], FIXED pos [XYZ])
{
	slTranslate (pos [X], pos [Y], pos [Z]);
	slRotX (ang [X]);
	slRotY (ang [Y]);
	slRotZ (ang [Z]);
}

void ss_main (void)
{
	static ANGLE ang1 [XYZ], ang2 [XYZ];
	static FIXED pos1 [XYZ], pos2 [XYZ];
	static ANGLE tmp = DEGtoANG (0.0);

	slInitSystem (TV_320x224, NULL, 1);
	slPrint ("Sample program 5.2", slLocate (6,2));

	ang1 [X] = ang2 [X] = DEGtoANG (30.0);
	ang1 [Y] = ang2 [Y] = DEGtoANG (45.0);
	ang1 [Z] = ang2 [Z] = DEGtoANG (0.0);

	pos2 [X] = toFIXED (DISTANCE_R2);
	pos2 [Y] = toFIXED (0.0);
	pos2 [Z] = toFIXED (0.0);
	while (-1) {
		slUnitMatrix (CURRENT);

		slPushMatrix ();
		{
			pos1 [X] = DISTANCE_R1 * slSin (tmp);
			pos1 [Y] = toFIXED (30.0);
			pos1 [Z] = toFIXED (220.0) + DISTANCE_R1 * slCos (tmp);
			set_star (ang1, pos1);
			slPutPolygon (& PD_CUBE);

			slPushMatrix ();
			{
				set_star (ang2, pos2);
				slPutPolygon (& PD_CUBE);
			}
			slPopMatrix ();
		}
		slPopMatrix ();

		ang1 [Y] + = DEGtoANG (1.0);
		ang2 [Y]-= DEGtoANG (1.0);
		tmp + = DEGtoANG (1.0);

		slSynch ();
	}
}

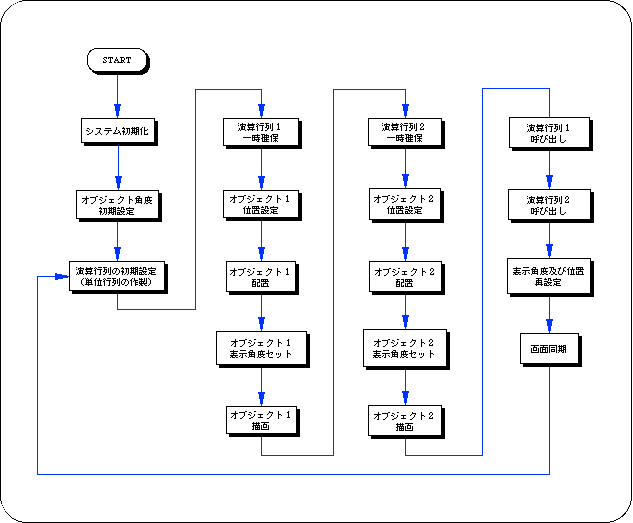
Flow 5-1 sample_5_2: Hierarchical matrix definition flowchart

5-3. Matrix function

In addition to the above, SGL supports the following functions as library functions related to matrix operations.

[Void slLoadMatrix (MATRIX mtptr)]

Copies the matrix specified as a parameter to the current matrix. Assign the MATRIX type variable of the specified matrix to the parameter.

[Void slGetMatrix (MATRIX mtptr)]

Copies the current matrix to the matrix specified as a parameter. Assign the MATRIX type variable of the specified matrix to the parameter.

[Void slMultiMatrix (MATRIX mtrx)]

Multiplies the current matrix by the matrix specified as a parameter. Assign the MATRIX type variable of the specified matrix to the parameter.

[Bool slPushUnitMatrix (void)]

Allocate the identity matrix on the stack and use it as the current matrix.
The previous current matrix is temporarily stored at a higher level in the stack.

[Void slUnitMatrix (MATRIX mtptr)]

Makes the matrix specified as a parameter an identity matrix. Assign the MATRIX type variable of the specified matrix to the parameter.
Also, only when "CURRENT" is assigned to the parameter, the target matrix becomes the current matrix, which enables the initialization of the current matrix.

Appendix SGL library functions that appeared in this chapter

In this chapter, the functions in the following table are explained.

Table 5-1 SGL library functions appearing in this chapter

Functional type	Function name	Parameters	function
void	slLoadMatrix	MATRIX mtpr	Copy the specified matrix to the current matrix
Bool	slPushMatrix	void	Temporary securing of matrix
Bool	slPushUintMatrix	void	Temporarily reserve the identity matrix on the stack
void	slGetMatrix	MATRIX mtpr	Copy the current matrix to the specified matrix
void	slInitMatrix	void	Initialization of matrix variables and buffers
void	slMultiMatrix	MATRIX mptr	Multiply the current matrix by the specified matrix
Bool	slPopMatrix	void	Restoration of temporarily saved matrix
void	slUintMatrix	MATRIX mptr	Make the specified matrix an identity matrix